Alexander Mikhailichenko

Interaction of multi-bunch beam with external cavity discussed since the times of damping rings design beginning (middle of sixties). Now, thirty-five years later, this problem looks hardly easier, however. New interest to this problem associated with B-factories, under construction around the world.

Usually for description of multi-bunch system the same techniques is used, as for description of a single bunch dynamics. The only difference is in presentation of the whole circulating current as a sum of Fourier components. So in this method it is difficult sometimes to separate the only one particular mode and it is practically impossible to distinguish higher order mode excitations (quadrupole, etc).

Here, in this publication, for description of multi-bunch system, containing q bunches, we used q functions of distribution fa , {} in it’s individual phase space. This phase space is now a non-interlaced junction of q independent sets of variables action-phase. The variables, describing the cavity, remain sensitive to the azimuthal phase of each individual bunch, however. Resulting current density is a sum of individual currents of each bunch, as - this is similar to usual techniques, but with not interlaced phase spaces. This simple method allowed easiest consideration of the problem.

Let us remind, first, how to solve a problem in general. Equation for distribution function f in a phase space is the following

. (1)

Here is the focusing force (+RF) and is the interactive force from the fields, induced by the beam in external cavity,–is a speed of particles. Lagrangian V can describe the beam-cavity interaction as the following

, , (2)

where –is a vector-potential, which satisfy the equation,

, (3)

where c–is a speed of light, –is a current density.

Equations (1) and (3) are self-consistent for definition and . Basically these equations known as Vlasov equations. Method of solution of these equations under specific requirements of accelerator physics was developed in [1]. We will follow this technique in our description of multi-bunch interaction with a cavity.

Let us consider, first, the case with a single bunch only. Deviation of momenta and phase from equilibrium ones defined by the following equations [2]

,

(4)

, , .

Here , –is a constant, –is an average radius of the ring, –is a longitudinal mass of the particle, –is a revolution frequency, –is a frequency of small oscillations, –is an equilibrium phase. Synchrotron mass and the frequency W defined as the following

, , (5)

where . For longitudinal dynamics only the phase space shrinks to one dimension (two variables). For easiest utilization, let us rewrite equation (1) with variables – action-phase. Hamiltonian now looks like . Under these variables (1) becomes

, (6)

where –is an instant synchrotron tune shift. Let us represent the distribution function as the following [1]

, (7)

where

, . (8)

Let us also represent Lagrangian as the following

(9)

Substitute (8) and (9) into (6) we can obtain

(10)

For obtaining (10) it was suggested, that the interaction is weak, so the spectrum of perturbation is close to non-perturbed one , . This allowed in presentation

(11)

to keep harmonic with l=0 only, as the input of remaining terms is of the order [1]. We also neglected the instant frequency shift .

Let us now represent as a function of . We shall use for this purpose (3). In our case of interest describes the field in the cavity, localized in azimuthal direction. Solution of (3) we are looking as a sum of eigenvectors like the following

(12)

, , ,

where integration is going over the volume of the cavity. From (3) one obtains

(13)

Representing

(14)

and substitute (14) into (13) one can find

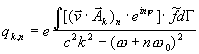(15)

So now one can find, substituting (15) into (14) and further into (12)

.

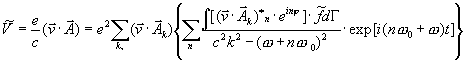Substitute this in (10) one can obtain an integral equation for as the following

(16)

To take into account the dissipation in the cavity one can introduce the imaginary part in frequency , where parameters of decrement is defined through partial quality factor, (do not mix this with variable Q_k from (12)).

Combining a moment

, (17)

one can obtain from (16) the following equation for moments

, (18)

where

.

If we neglecting the spread over synchrotron frequencies W , we can consider the simplest equilibrium distribution f₀(I) as the following

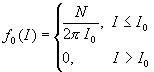. (19)

As one can see from expansion , where J_m –is a Bessel function,

. (20)

Substituting (20) and (19) into (18) and further in (17) one can obtain

(21)

and for equation for momenta (17) one can obtain

. (22)

If we suppose that resonant condition is satisfied for only one harmonics , then the last equation (22) could be simplified as to

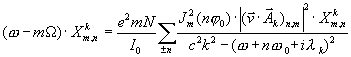(23)

where in summation means, that there are only two terms: +n and -n only. Let us combine two terms as the following

. (24)

With (24) the main equation (22) could be transferred into

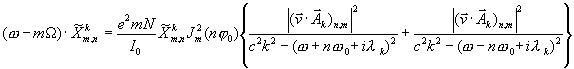
(25)

Substitute in denominator in (25) , one can finally find a decrement as

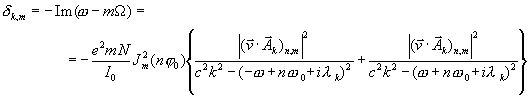. (26)

For longitudinal velocity of the particle we have an expression . For azimuthal component of the impedance on particular harmonics of revolution we have (see Appendix for details)

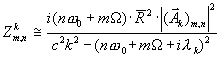. (27)

So, one comes to a decrement like the following

. (28)

Taking into account (4) and (5), (28) yields a final expression

, (29)

where –is an average beam current and –is a real part of impedance. For dipole oscillations, m=1. Expanding , one can find a decrement as

. (30)

One can easily recognize here a Robinson’s formula. Meanwhile our solution (29) gives the decrement for any higher moment above the dipole one, m >1. Physical sense of (30) is clear. This is a difference in losses of slow and fast phase wave running along the trajectory. Above the critical energy slow wave (low band width line) corresponds to the particles having higher energy in it’s synchrotron oscillation. Fast wave –to the low energy particles. System is stable if particle, acquired higher energy also radiates more. Due to synchrotron oscillation and constant exchange interaction with slow and fast wave there appears a difference in balance. All this becomes clear if (30) is rewritten in the following way

,

where –is a side band voltage, –is a full energy acquired by equilibrium particle.

In case of multi-bunch beam, situation becomes the following. If the harmonics number of RF is q, , then q bunches can be placed into the same orbit. Let us introduce q functions of distribution . These functions describe the distribution of particles in the phase space of each bunch. Zero phases for each bunch can be described by the following obvious expression

, (31)

where we introduced the equilibrium phase for each bunch as . This presentation defines the only equilibrium location of the bunch along the azimuth. Now resulting current is a sum of individual currents of each bunch, as . Some of the currents in this sum could be equal to zero.

If we suppose that the frequencies of longitudinal oscillations differs a little, so in sum current one can neglect the terms with beat frequencies, one can obtain a system of equations like (16)

,

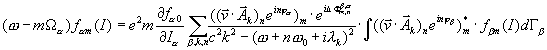(32)

where . One can see from here, that decrements will depend in general case on the initial phase distribution, . For the point like bunches, oscillating as rigid bodies, the phase differences defined so called normal modes of oscillation. Let us suggest that . Let us suggest also, that equilibrium distributions are homogeneous again like

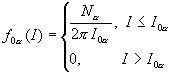. (33)

Supposing finally, that , we are coming to a system for determination

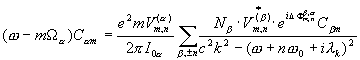, (34)

where and, again we leave the only resonant term . We also supposed that . One can see from (34) that a resulting spectrum for each bunch, defined by the others ones in the same manner as the bunch itself influence to this process. Arranging a moment

, (35)

where , one can find from (34) that

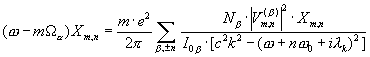. (36)

Substitute here for simplicity , , one cane obtain for a decrement

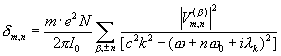, (37)

or

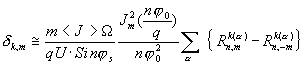. (38)

One can see from here that the resulting decrement for any particular mode is a sum of individual decrements of each bunch. This result was obtained for the first time in [3].

Formula (38) could be considered in terms of more general theorem on sum of decrements, what states that for system of oscillators, sum of decrements does not depend on the oscillator coupling [4]. In that context it is clear also, that dispersion equation for a single bunch (29) has the same view as (38). Basis for formula (38) could be understood also as the following. As we represented current as a vector joint, the voltage induced in external cavity could be represented as . The sum in this expression could be also treated as a sum over orthogonal components, corresponding to the normal modes. For dipole oscillations the number of these modes is also equal to q. The spectral power density could be represented as . All cross terms are vanished, due to absence of pair correlation .

For treatment of (38) we can also say that the power acquired from RF and dissipated into a parasitic cavity will not depend on how close to each other in azimuthal direction the bunches are running. The coupling between bunches redistribute the decrement only.

We made some assumptions. How strong they are? Rectangular distribution in action as (19), (33) gave the simplest way to make integration, as in this case what was substituted in (18). Any other equilibrium distribution, like say, Gaussian, brings equations (18) to the

, (18a)

where

And if we neglect the tune shift dependence over action, , then result will be the same if one substitutes .

We suggested also that . One can indeed suggest that some of the numbers are zero. This means, that the bunch is missed here. With this way one can investigate any desirable bunch pattern. In this case formula (37) becomes

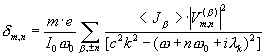, (37a)

where –is an average current of each individual bunch.

One can see, that in general case decrement and a tune shift is a function of the bunch size, 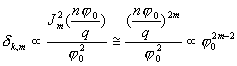. Only for dipole oscillations, m =1 this is not so. Real part of (26), gives the tune shift as

(39)

what gives, in principle, an idea on how tune shift depends on the beam size.

One can see from (38) and (39) that the decrement and tune shift linearly depend on current. Meanwhile for general mode, , experimentally was found [5] that there is significant nonlinear (quadratic) term in shift-current dependence. This was explained by the work of RF feedback system, which mechanically shifts the cavity resonant frequency so that this adjusts the RF property of the cavity from the side of RF transceiver [5] ( are changing while the current is changing). Really, in the presence of the beam, some RF power is going out from RF cavity with the beam. This could be described by a quality factor, associated with the beam -- . Really, the impedance of the cavity from the side of RF generator, could be described by the same formula for impedance, except other loop of integration of eigenvectors . In the presence of the beam the effective quality factor becomes , and the impedance looks as the following

.

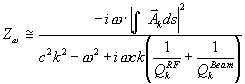Here integration is going along the loop of excitation of the cavity. In case if excitation of the cavity is going through the window (hole), one needs to replace , where is the magnetic field configuration in the region of the window. So one can see, that variation in could be compensated by change of main cavity frequency . One can see that his dependence is nonlinear. Ignoring this feedback system influence to the process, sometimes might be a source of confusion.

For the counter-rotating beams of positrons and electrons one can use the same formulas for decrement. One could see that the way these equations were obtained has a deal with two counter-rotating angular harmonics, carrying sub-harmonics, associated with sidebands.

One can easily estimate the influence of other assumptions made here.

[1] Ya.S. Derbenev, N.S. Dikansky, "On the damping of Coherent Oscillations of a Beam

in a Storage Ring", Preprint INP 69-315, Novosibirsk, 1969.

[2] A.A. Kolomensky, A.N.Lebedev, " Theory of Cyclic Accelerators", J.W.&S. Inc., NY,

1966.

[3] A.A. Mikhailichenko, "Investigation of Coherent Beam oscillations in a Synchrotron",

MD Thesis, Novosibirsk State University, 1971.

[4] N.S. Dikansky, D.V. Pestrikov, "The Physics of Intense Beams and Storage Rings",

AIP Press, NY, 1994, p.117.

[5] S. Belomestnykh, " Coherent Synchrotron Frequency Shift due to Fundamental

Accelerator Cavity Mode", SRF 970314-01.

Let us introduce impedance of the cavity as the following. Substitute (12) into (3) and multiplying both sides by , one can obtain after integrating over the volume

. (13a)

Suggesting here that the beam have transverse dimensions much smaller, than the transverse distance, where is changing, one can integrate over transverse cross-section and obtain

,

where J(t) –is an instant current. Representing , one can obtain

(15a)

For the voltage along the trajectory one can obtain

.

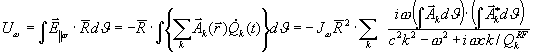So the impedance could be defined as

,

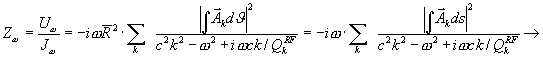
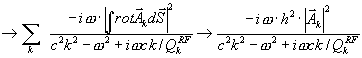where —is the element of the area circled by the way of integrating, h—is an effective length of the cavity gap, — is a longitudinal coordinate. In last expression we omitted all harmonics, but one. In our case . Basically we supposed, however, that . As the magnetic field , one can see from last expression that impedance is proportional to the flux, captured by the (trajectory) loop. The view of impedance what is more familiar for electrical engineers could be transferred from our expression as the following

,

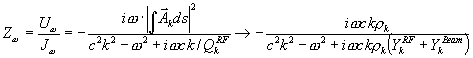where —is so called wave resistance (depending on the cavity geometry only), —is so called conductivity of the cavity, , where —is an effective Q -factor associated with the beam, —is so called conductivity of the beam. In the absence of beam, on the resonant frequency , the impedance is active, . Impedance could be rewritten as a sum of real and imaginary parts

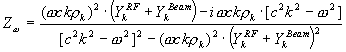
Usually and contains active and real part also. Really . And , where –is electromagnetic energy stored in the mode and –is the power, carried out by the beam. The last one could be calculated as the following

,

where transit time factor included in voltage U. Energy of electromagnetic field calculated as usual . As usual, , . One can see that the quality factor, associated with the beam, is a linear function of the current in the lowest order.